Paul J. Wright

DeepEM

A Deep Learning Approach for DEM Inversion

The intensity observed through optically-thin SDO/AIA filters (94 Å, 131 Å, 171 Å, 193 Å, 211 Å, 335 Å) can be related to the temperature distribution of the solar corona (the differential emission measure; DEM) as

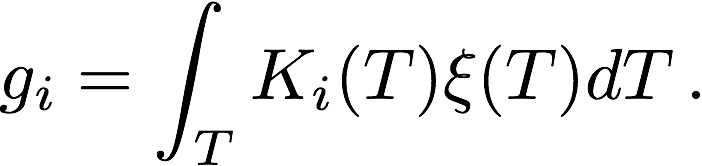
In this equation, g_i is the DN/s/px value in the ith SDO/AIA channel. This intensity corresponds to the K_i(T) temperature response function, and the DEM, ξ(T), is in units of cm^-5 K^-1. The matrix formulation of this integral equation can be represented in the form, g = Kξ, however, this problem is an ill-posed inverse problem, and any attempt to directly recover ξ leads to significant noise amplication.

There are numerous methods to tackle mathematical problems of this kind, and there are an increasing number of methods in the literature for recovering the differential emission measure. These include methods based techniques such as Tikhonov Regularisation (Hannah & Kontar 2012), or on the concept of sparsity (Cheung et al 2015).

In this notebook (DeepEM.ipynb) we will introduce a deep learning approach for Differential Emission Measure (DEM) Inversion. For this notebook, DeepEM is a trained on one set of SDO/AIA observations (six optically-thin channels; 6 x N x N) and DEM solutions (in 18 temperature bins from log_{10}T = 5.5 - 7.2 K, 18 x N x N; Cheung et al 2015) at a resolution of 512 x 512 (N = 512) using a 1x1 2D Convolutional Neural Network with a single hidden layer.

The DeepEM method presented here takes every DEM solution with no regards to the quality or existence of the solution. As will be demonstrated, when this method is trained with a single set of SDO/AIA images and DEM solutions, DeepEM solutions have a similar fidelity to Basis Pursuit (with a significantly increased computation speed—on the order of 10 million DEM solutions per second), and additionally, DeepEM finds positive solutions for every pixel, and reduced noise in the DEM solutions.

This notebook was developed with PyTorch, and is available at https://github.com/PaulJWright/DeepEM

DeepEM Gif — **Figure 1:** Example of the `DeepEM` solution for log_{10}T ~ 5.9 K and 6.3 K, in comparison to the Basis Pursuit solution, and the *SDO*/AIA images for the same temperature.

This project was initiated during the 2018 NASA Frontier Development Lab (FDL) program, a partnership between NASA, SETI, NVIDIA Corporation, Lockheed Martin, and Kx. We gratefully thank our mentors for guidance and useful discussion, as well as the SETI Institute for their hospitality.